what angle measure in radians corresponds to rotations around a circle

\(\require{abolish}\newcommand\caste[0]{^{\circ}} \newcommand\Ccancel[two][black]{\renewcommand\CancelColor{\color{#i}}\cancel{#2}} \newcommand{\alert}[one]{\boldsymbol{\colour{magenta}{#one}}} \newcommand{\blert}[1]{\boldsymbol{\color{blue}{#1}}} \newcommand{\bluetext}[ane]{\color{blueish}{#one}} \delimitershortfall-1sp \newcommand\abs[1]{\left|#1\right|} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \)

In the previous section, nosotros introduced periodic functions and demonstrated how they can be used to model real life phenomena like the rotation of the London Centre. In fact, at that place is an intuitive connection betwixt periodic functions and the rotation of a circle. In this section, nosotros will use our intuition and formalize this connection by exploring the unit circle and its unique features that atomic number 82 united states into the rich world of trigonometry.

Many applications involving circles also involve a rotation of the circle so we must first introduce a mensurate for the rotation, or angle, between two rays (line segments) emanating from the center of a circle.

The measure of an angle is a measurement between 2 intersecting lines, line segments, or rays, starting at the initial side and ending at the terminal side. Information technology is a rotational measure, not a linear measure.

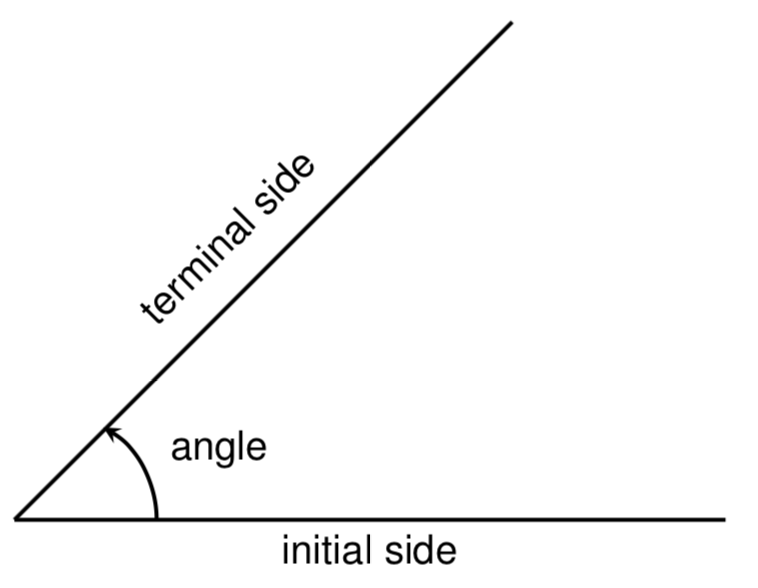
When measuring angles on a circle, unless otherwise directed, nosotros mensurate angles in standard position: starting at the positive horizontal axis with a counterclockwise rotation.

Subsection Measuring Angles in Degrees

A degree is a unit of measurement of an angle. One rotation around a circle is equal to 360 degrees.

An angle measured in degrees should always include the degree symbol \(^\circ\) or the word "degrees" later on the number. For instance, \(ninety^\circ=90\) degrees.

Example 6

Give the degree measure of the angle shown on the circle.

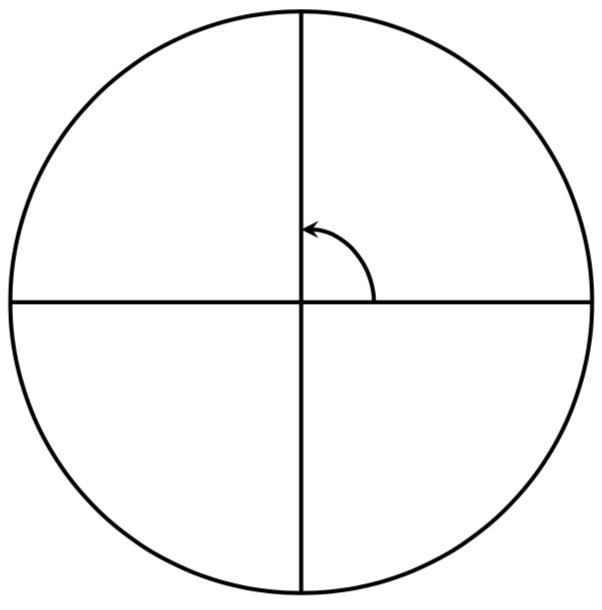
Solution

The vertical and horizontal lines dissever the circle into quarters. Since one full rotation is 360 degrees, each quarter rotation is \(360^\circ / iv = 90^\circ\text{.}\)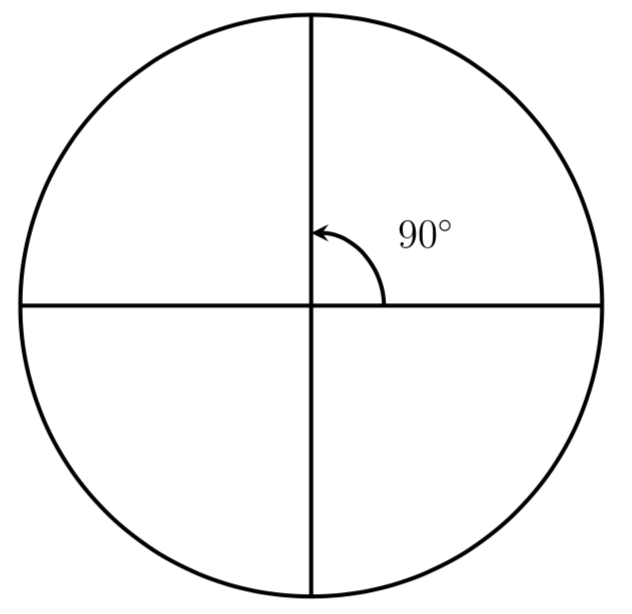

Example 7

Describe an angle of \(30^\circ\) on a circle.

Solution

An bending of \(30^\circ\) is \(ane/iii\) of \(90^\circ\) so by dividing a quarter rotation into thirds, we tin can describe a line showing an bending of \(30^\circ\text{.}\)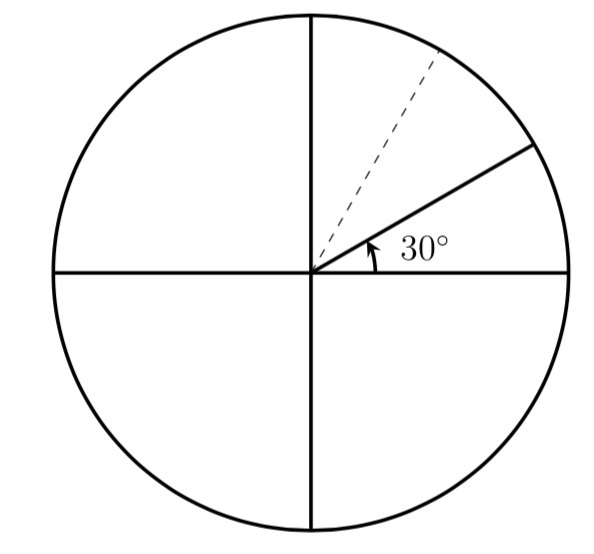

Find that since at that place are 360 degrees in one rotation, an angle greater than 360 degrees would indicate more than one full rotation. Shown on a circumvolve, the resulting direction in which this angle'south last side points is the aforementioned equally some other for an angle between 0 and 360. These angles are called coterminal.

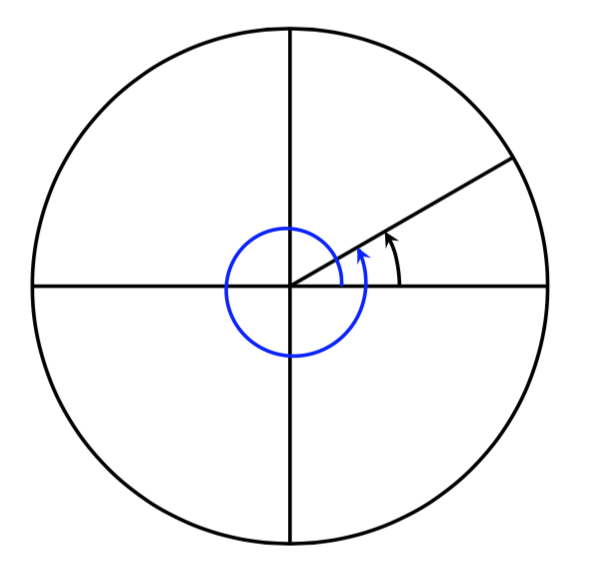
Later on completing their full rotation based on the given angle, two angles are coterminal if they finish in the aforementioned position, then their terminal sides coincide (bespeak in the same direction).

Example 9

Detect an bending \(\theta\) that is coterminal with \(800^\circ\) where \(0^\circ \leq \theta \lt 360^\circ \text{.}\)

Solution

Since adding or subtracting a full rotation, or 360 degrees, would result in an angle with the terminal side pointing in the same direction, nosotros can find coterminal angles by adding or subtracting 360 degrees.

An angle of 800 degrees is coterminal with an bending of

\begin{equation*} 800^\circ - 360^\circ = 440^\circ \finish{equation*}

It is also coterminal with an bending of

\begin{equation*} 440^\circ - 360^\circ = 80^\circ\text{.} \end{equation*}

Finding the coterminal bending between 0 and \(360^\circ\) tin can make it easier to see which direction the terminal side of an angle points in.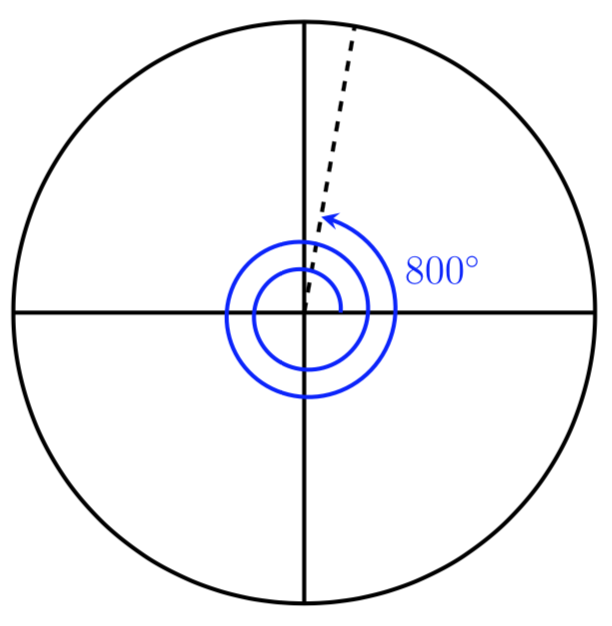

Example 10

Discover an angle \(\blastoff\) that is coterminal with \(870^\circ\) where \(0^\circ \leq \alpha \lt 360^\circ \text{.}\)

Solution

To discover angles with the terminal sides pointing in the same direction, nosotros tin can decrease 360 degrees:

\begin{equation*} \begin{aligned} 870^\circ-360^\circ \amp= 510^\circ \\ 510^\circ-360^\circ \amp= 150^\circ \finish{aligned} \end{equation*}

Therefore \(870\) degrees is coterminal with \(150\) degrees.

Example 12

Draw an angle of \(-45^\circ\) on a circle and detect a positive coterminal angle \(\alpha\) where \(0^\circ \leq \alpha \lt 360^\circ \text{.}\)

Solution

Since 45 degrees is one-half of xc degrees, nosotros can start at the positive horizontal centrality and measure out clockwise half of a 90 degree bending.

We can find a positive coterminal bending by adding 360 degrees.

\begin{equation*} -45^\circ+360^\circ=315^\circ \end{equation*}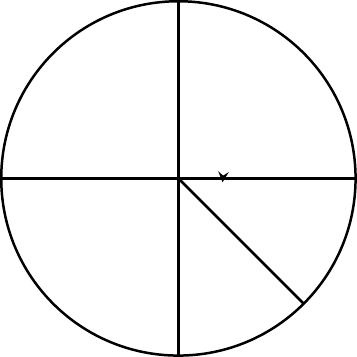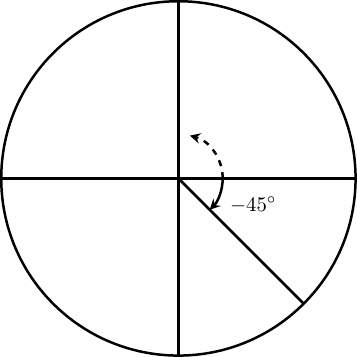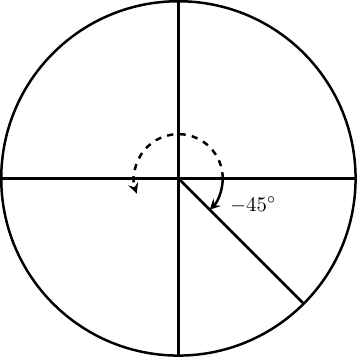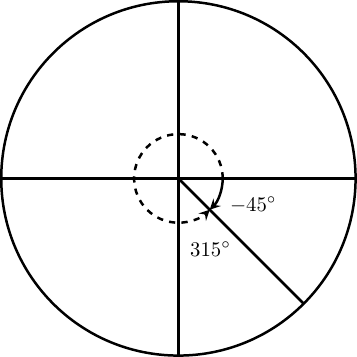

Example 13

Find an bending \(\beta\) that is coterminal with \(-300^\circ\) where \(0^\circ \leq \beta \lt 360^\circ \text{.}\)

Solution

Since \(-300^\circ+360^\circ=60^\circ\text{,}\) \(60\) degrees is coterminal with \(-300^\circ\text{.}\)

Subsection Measuring Angles in Radians

While measuring angles in degrees may exist familiar, doing so oft complicates matters since the units of measure tin can become in the way of calculuations. For this reason, another measure of angles is unremarkably used. This measure is based on the distance effectually the unit circle.

The Unit Circumvolve

The unit circumvolve is a circle of radius ane, centered at the origin of the \((x,y)\) plane. When measuring an angle effectually the unit circumvolve, we travel in the counterclockwise management, starting from the positive \(x\)-axis. A negative angle is measured in the opposite, or clockwise, management. A consummate trip around the unit circle amounts to a total of 360 degrees.

A radian is a measurement of an angle that arises from looking at angles as a fraction of the circumference of the unit of measurement circle. A consummate trip around the unit circle amounts to a total of \(2\pi\) radians.

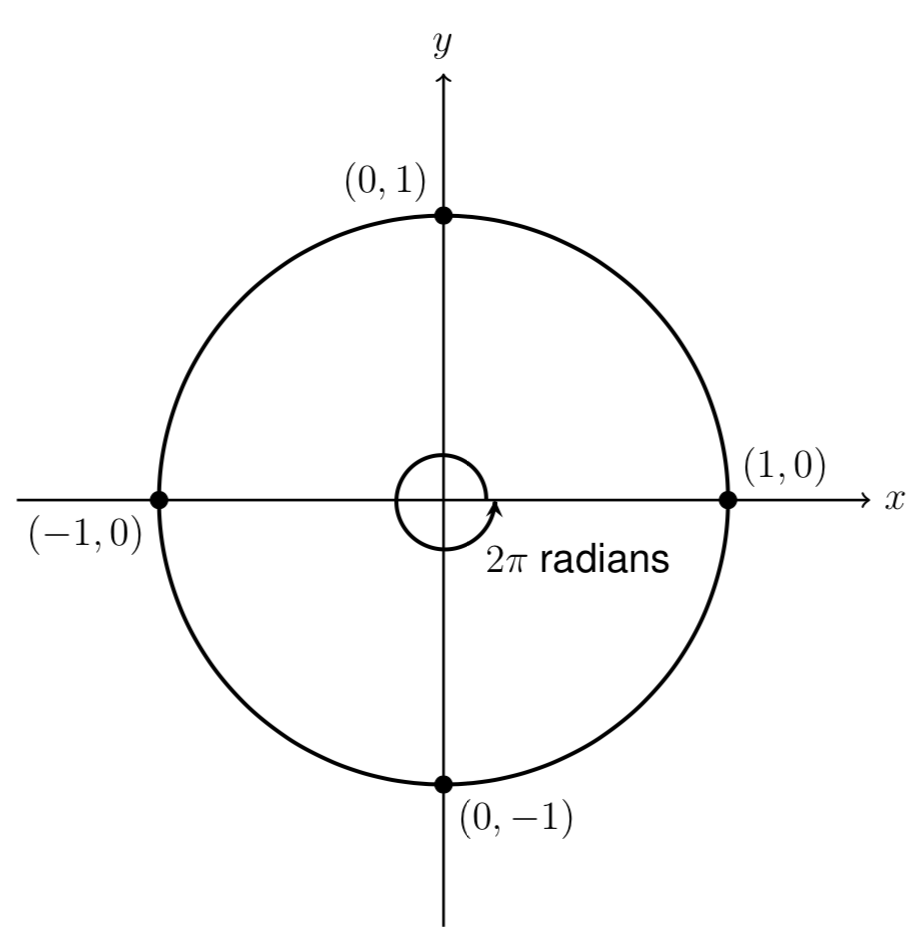
Radians are a unitless measure. Therefore, it is not necessary to write the label "radians" after a radian measure, and if you see an angle that is not labeled with "degrees" or the degree symbol, y'all should assume that it is a radian measure.

Radians and degrees both measure angles. Thus, information technology is possible to convert between the ii. Since one rotation around the unit circle equals 360 degrees or \(2\pi\) radians, nosotros can use this as a conversion factor.

Converting Between Radians and Degrees

Since \(360 \text{ degrees} = 2\pi \text{ radians}\text{,}\) nosotros tin can dissever each side by 360 and conclude that

\begin{equation*} \displaystyle one \text{ degree} = \frac{2\pi \text{ radians}}{360} = \frac{\pi \text{ radians}}{180} \end{equation*}

So, to convert from degrees to radians, we can multiply by \(\displaystyle \ \frac{\pi \text{ radians}}{180^\circ}\)

Similarly, we can conclude that

\begin{equation*} \displaystyle 1 \text{ radian} = \frac{360^\circ}{two\pi} = \frac{180^\circ}{\pi} \finish{equation*}

So, to convert from radians to degrees, we tin multiply by \(\displaystyle \ \frac{180^\circ}{\pi \text{ radians}}\)

Case 15

Convert \(\displaystyle \frac{\pi}{vi}\) radians to degrees.

Solution

Since we are given an bending in radians and we want to catechumen it to degrees, we multiply the bending by \(180^\circ\) and so divide past \(\pi\) radians.

\brainstorm{equation*} \frac{\pi}{6} \text{ radians} \cdot \frac{180^\circ}{\pi \text{ radians}} = thirty^\circ \stop{equation*}

Example 16

Catechumen \(15^\circ\) to radians.

Solution

In this example, nosotros start with an angle in degrees and want to convert it to radians. We multiply by \(\pi\) and split up past \(180^\circ\) and then that the units of degrees cancel and we are left with the unitless measure of radians.

\begin{equation*} 15^\circ \cdot \frac{\pi}{180^\circ} = \frac{\pi}{12} \cease{equation*}

Example 17

Catechumen \(\displaystyle \frac{7\pi}{ten}\) radians to degrees.

Solution

Since we are given an angle in radians and we want to convert it to degrees, we multiply by the bending \(180^\circ\) and then split up past \(\pi\) radians.

\begin{equation*} \frac{vii\pi}{x} \text{ radians} \cdot \frac{180^\circ}{\pi \text{ radians}} = 126^\circ \end{equation*}

Above, we explored how to find coterminal angles for angles greater than 360 degrees and less than 0 degrees. Similarly, we tin can find coterminal angles for angles greater than \(2\pi\) radians and less than 0 radians.

Example 19

Find an angle \(\beta\) that is coterminal with \(\displaystyle \frac{xi\pi}{four}\) where \(0^\circ \leq \beta \lt 2\pi \text{.}\)

Solution

When working in degrees, we constitute coterminal angles by calculation or subtracting 360 degrees, a full rotation. Besides, in radians, we can find coterminal angles past adding or subtracting full rotations of \(2\pi\) radians.

An angle of \(11\pi/iv\) is coterminal with an angle of

\begin{equation*} \frac{11\pi}{4} - two\pi = \frac{eleven\pi}{iv} - \frac{8\pi}{4} = \frac{three\pi}{iv} \end{equation*}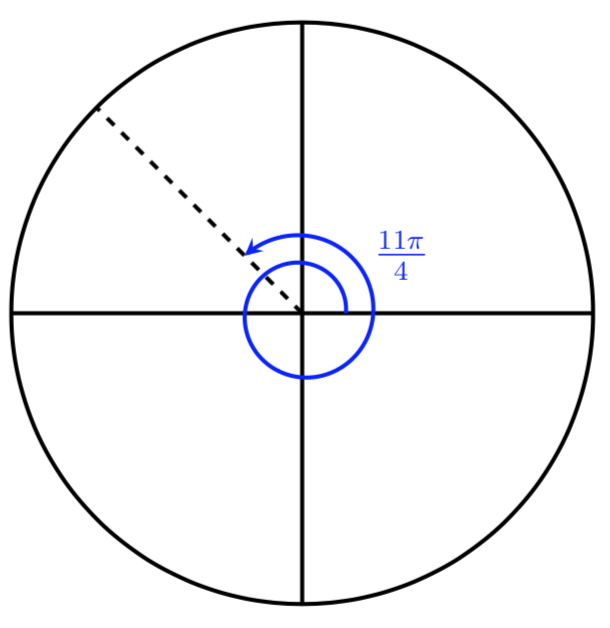

Example 20

Find an angle \(\phi\) that is coterminal with \(\displaystyle -\frac{11\pi}{6}\) where \(0^\circ \leq \phi \lt 2\pi \text{.}\)

Solution

An angle of \(-\frac{11\pi}{6}\) is coterminal with an angle of

\brainstorm{equation*} -\frac{11\pi}{6} + two\pi = -\frac{eleven\pi}{6} + \frac{12\pi}{6} = \frac{\pi}{vi} \end{equation*}

Subsection Finding Points on the Unit of measurement Circle

While it is convenient to describe the location of a point on the unit circle using an angle, relating this angle to the \(x\) and \(y\) coordinates of the corresponding indicate is an important application of trigonometry. To practise this, we volition demand to utilise our knowledge of triangles.

Case 21

Observe the \((x,y)\) coordinates for the bespeak on the unit circumvolve corresponding to an bending of 45 degrees or \(\pi/4\) radians.

Solution

Let's showtime past cartoon a picture and labeling the known information.

We want to find the \(10\) and \(y\) coordinates of the point on the unit circle corresponding to an angle of 45 degrees or \(\pi/4\text{.}\) To do this, nosotros tin can depict a vertical line from the indicate down to the \(ten\)-centrality, which forms a correct triangle. The hypotenuse of this triangle is 1, since it corresponds to the radius of the unit circle, and the side lengths of this triangle are equal to \(x\) and \(y\text{.}\)

Now, using the Pythagorean Theorem, nosotros get that

\brainstorm{equation*} ten^ii+y^2=i^2 \hspace{.25in} \text{ which simplifies to } \hspace{.25in} x^two+y^2=1 \terminate{equation*}

Since the triangle formed is a 45-45-90 degree triangle, side lengths \(ten\) and \(y\) must be equal. Therefore, we can substitute in \(x=y\) into the above equation.

\begin{align*} x^2+y^2 \amp = 1 \amp\amp \text{Substitute in } x=y \\ \\ x^2+10^2 \amp = one \amp\amp \text{Add similar terms } \\ \\ 2x^2 \amp = 1 \amp\amp \text{Divide by ii} \\ \\ x^2 \amp = \frac{i}{2} \amp\amp \text{Take the square root} \\ \\ ten \amp = \pm\sqrt{\vphantom{\frac{i^ii}{2}}\frac{i}{two}} \amp\amp \text{Since the } ten \text{ value is positive, we keep the positive root so} \\ \\ x \amp = \sqrt{\vphantom{\frac{one^2}{2}}\frac{1}{2}} \amp\amp \stop{align*}

Ofttimes this value is written with a rationalized denominator. Recall that to rationalize the denominator, we multiply by a term equivalent to 1 to get rid of the radical in the denominator, and then

\begin{equation*} x = \sqrt{\vphantom{\frac{1^two}{2}}\frac{1}{ii}} \, \sqrt{\vphantom{\frac{i^2}{2}}\frac{2}{2}} = \sqrt{\vphantom{\frac{i^2}{2}}\frac{ii}{4}} = \frac{\sqrt{2}}{2} \end{equation*}

and since \(x\) and \(y\) are equal, \(\displaystyle y=\frac{\sqrt{ii}}{two}\text{.}\)

Thus, the \((ten,y)\) coordinates for the point on the unit circle corresponding to an angle of 45 degrees or \(\pi/4\) radians are

\begin{equation*} (x,y) = \left(\frac{\sqrt{ii}}{two},\frac{\sqrt{2}}{2}\correct)\text{.} \end{equation*}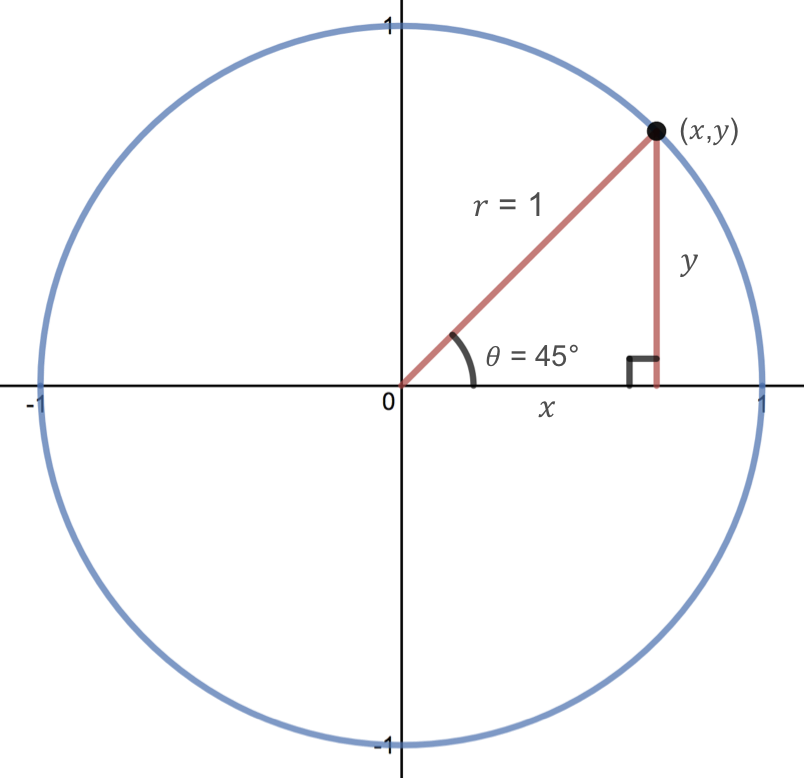

Example 22

Notice the \((x,y)\) coordinates for the point on the unit circle corresponding to an angle of thirty degrees or \(\pi/half-dozen\) radians.

Solution

Let'southward outset by drawing a movie and labeling the known information.

Nosotros want to find the \(ten\) and \(y\) coordinates of the point on the unit circle corresponding to an angle of 30 degrees or \(\pi/six\text{.}\) To do this, we can draw a triangle inside the unit circle with one side at an bending of 30 degrees and another at an angle of \(-xxx\) degrees.

Notice that if we combine the resulting ii right triangles to form i large triangle, and then all three angles of the larger triangle are equal to threescore degrees.

Since all of the angles in this triangle are equal, the sides will all be equal as well. Two of the side lengths of this triangle are equal to 1 considering they correspond to the radius of the unit of measurement circle. Thus, the other side length must besides be equal to 1. This side likewise has a length of \(2y\text{.}\) Therefore, we can conclude that \(2y = 1\) and so

\begin{equation*} y=\frac{1}{2} \end{equation*}

Now, nosotros can apply the Pythagorean Theorem to one of the right triangles to find the \(x\) value. We get that

\begin{align*} ten^two+y^2 \amp = 1^2 \\ \\ ten^two+\left(\frac{ane}{2}\right)^ii \amp = 1 \\ \\ x^two+\frac{1}{four} \amp = 1 \\ \\ x^ii \amp = \frac{3}{four} \\ \\ x \amp = \pm\sqrt{\vphantom{\frac{3^2}{four}}\frac{3}{4}} \\ \\ x \amp = \sqrt{\vphantom{\frac{3^2}{4}}\frac{3}{four}} = \frac{\sqrt{iii}}{ii} \end{align*}

Thus, the \((x,y)\) coordinates for the betoken on the unit of measurement circle corresponding to an angle of xxx degrees or \(\pi/6\) are

\begin{equation*} (10,y) = \left(\frac{\sqrt{iii}}{2},\frac{1}{2}\right)\text{.} \terminate{equation*}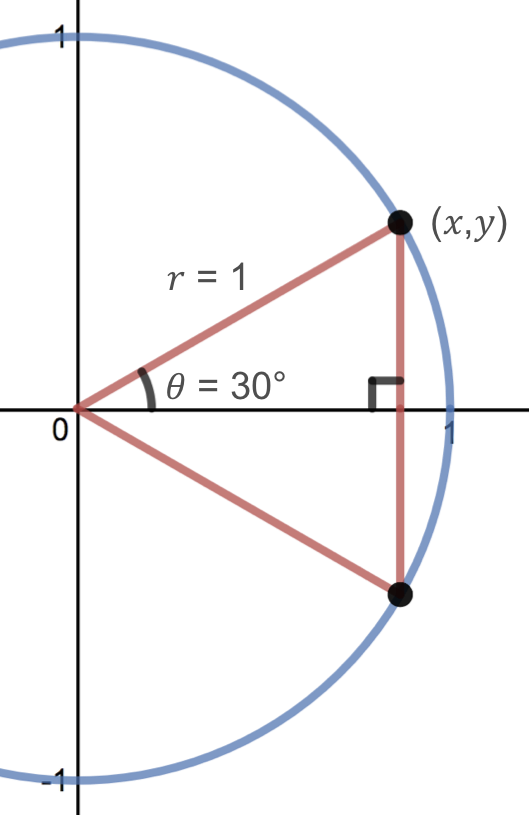

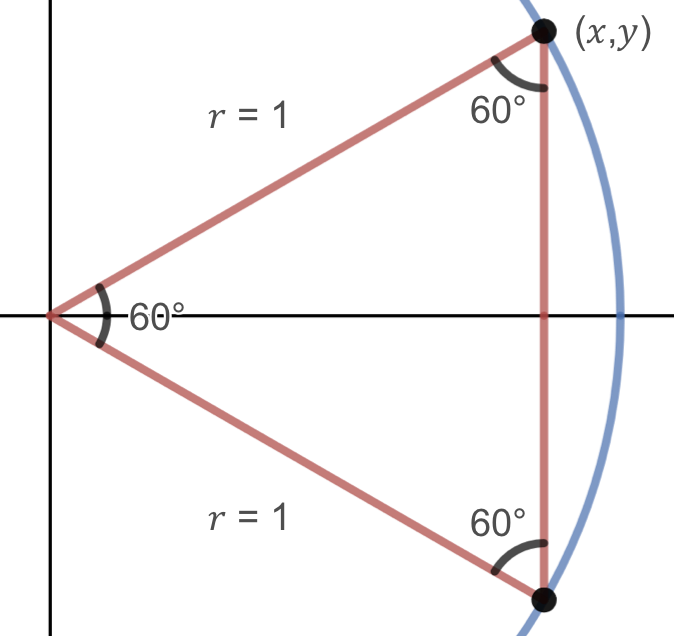
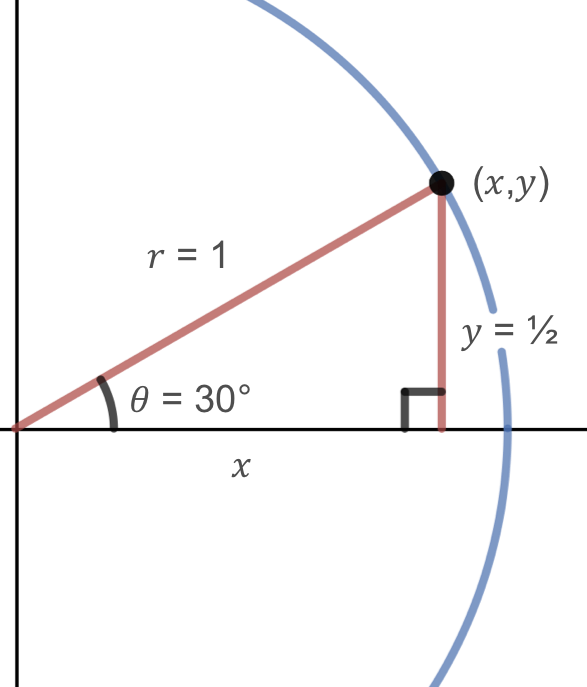
In the previous instance, we applied our cognition of triangles to find the \(x\) and \(y\) coordinates of the bespeak on the unit circle corresponding to 30 degrees. We can now use symmetry to detect the \(ten\) and \(y\) coordinates corresponding to an bending of 60 degrees or \(\pi/three\text{.}\) First, we describe a picture of the triangle corresponding to this bespeak on the unit of measurement circle.

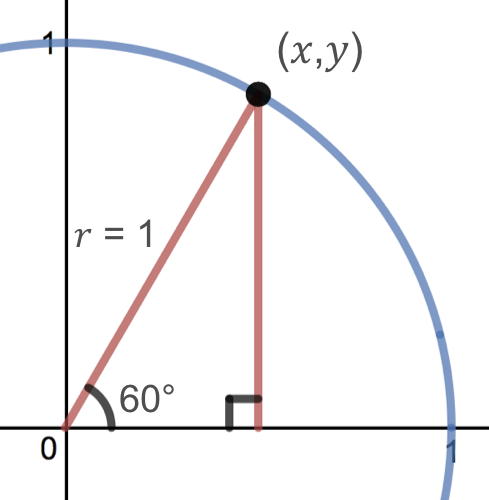
Observe that the triangle shown higher up is similar to the one formed by the 30 degree bending since the hypotenuse is the same length and both are xxx-60-90 caste triangles. Therefore, the \((x,y)\) coordinates for lx degrees are the same as the \((ten,y)\) coordinates for xxx degrees, only switched.

Thus, the \((ten,y)\) coordinates for the point on the unit circle respective to an angle of lx degrees or \(\pi/3\) are

\brainstorm{equation*} (10,y) = \left(\frac{1}{2},\frac{\sqrt{iii}}{ii}\correct)\text{.} \end{equation*}

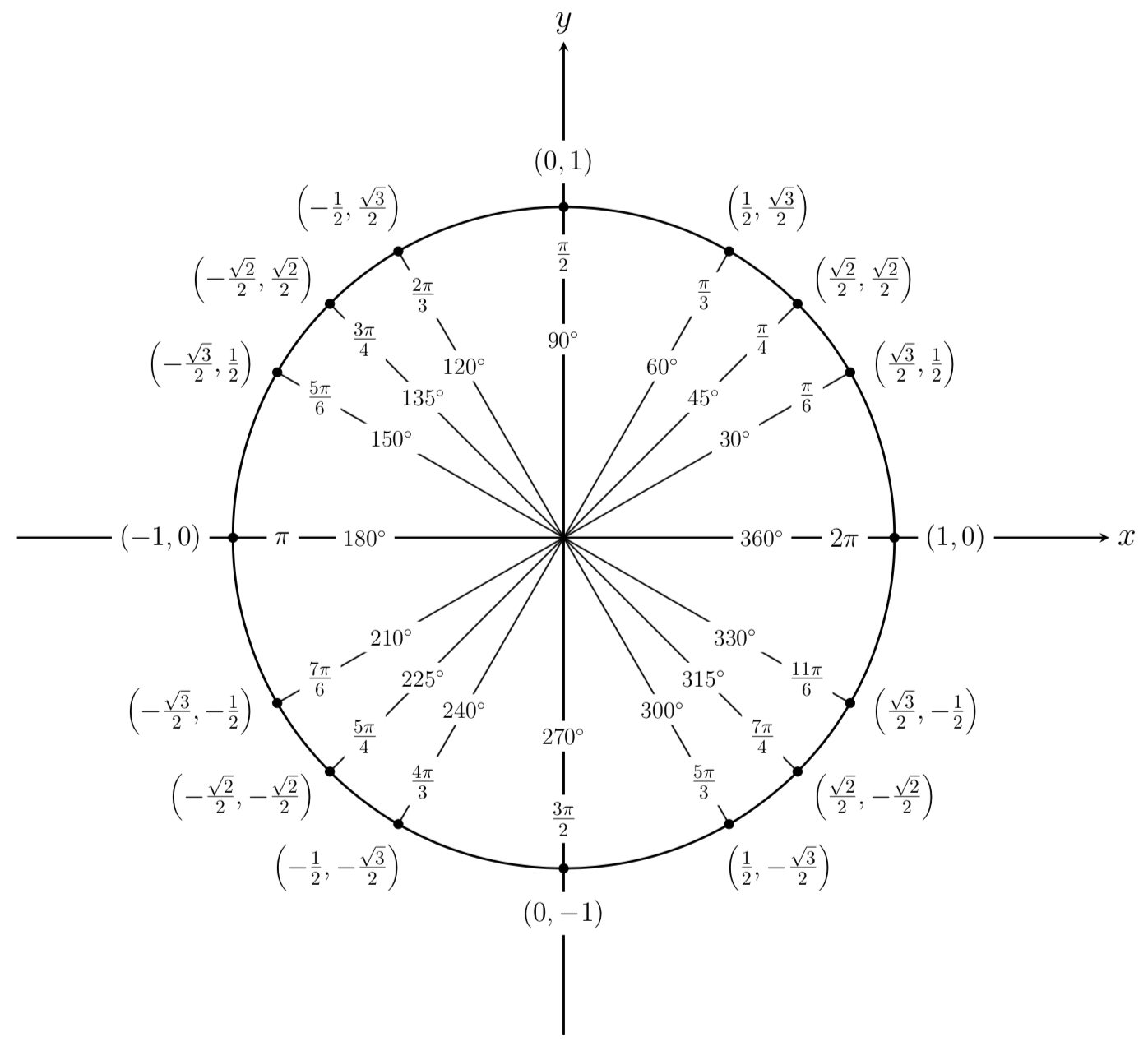
We have now found the coordinates of the points respective to all the commonly encountered angles in the first quadrant of the unit circle. Using symmetry, we can find the rest of the coordinates respective to common angles on the unit circle. A labeled picture of the unit circumvolve is shown below.

Subsection Supplemental Videos

• Measuring Angles
• Coordinates on the Unit Circle
• Examples

Subsection Exercises

1 Converting Degrees to Radians

2 Converting Radians to Degrees

3 Converting Between Degrees and Radians

iv Practical Converting Between Degrees and Radians

bryantsonew1991.blogspot.com

Source: https://mathbooks.unl.edu/PreCalculus/unit-circle.html

Share this post